Creating a Virtual Sundial with FME


This is the first of what I hope will be a three part article. While it’s not something you’re all going to rush out and copy, I hope the methods I use will be of use to you, and will illustrate new functionality in FME 2015.0 and 2015.1
If you follow me on Twitter you might already guess what my project is about: sundials!
What triggered this project is that FME 2015 got a new transformer called the SurfaceFootprintReplacer. As the name suggests, the primary use is to create a footprint from a 3D feature such as a building, like so (the footprint is offset in the Z axis so you can see it):
But really (and we might have to improve our terminology here) the transformer is all about creating shadows. A footprint is merely an ‘overhead’ shadow, but the transformer also has options for adding the direction of the light source, so that we can cast an oblique shadow.
Of course, one of the most famous items that casts a shadow is a sundial! So this post is about how I created a sundial using FME and the SurfaceFootprintReplacer. My following posts will (if I can get it to work) involve writing the sundial out to render it in three.js for viewing in a web browser, and then serving up that data using FME Server, to create an online virtual sundial.
This article goes into not just how I created this with FME, but also a bit of the theory behind sundials and why I chose the options I did. There’s a link to download the workspace at the foot of the article.
The Goal
What is a sundial? OK, we all know a sundial is a device for indicating time according to the sun’s position. But did you know that a sundial’s face varies according to the latitude of the location it is placed? If you buy a sundial from a shop, and you can’t adjust the angle to your latitude, then it’s nothing but a pretty garden ornament.
So, if I generate a sundial it’s face has to be latitude-specific. The question is (or was) what, exactly, am I trying to do here?
If I want my sundial to look *exactly* as it would if you looked out of your window and saw it, then it becomes complicated. I need to take the exact latitude and longitude of the viewer into account, generate the sundial layout within the workspace to match that lat/long, then factor in something called the equation of time. And after all that, you’d have a great sundial, but you would find it was telling “local apparent time”, which is greatly different to what the clock on your wall is saying.
But if all I want is an accurate representation of “standard” time – i.e. the sundial is simply a reflection of what appears on your clock/watch – then it’s less of a problem. I can pick any single latitude, as long as I stick to it, and the longitude will be fixed to the meridian for whatever time zone is chosen.
Sundial Construction
So the first task was to create the face of my sundial. This I did in Bentley MicroStation. Other CAD products are available(!) but I have more experience in MicroStation so chose that. I constructed the face using layout methods in a book called Sundials: Their Theory and Construction, and confirmed the result using this useful spreadsheet.
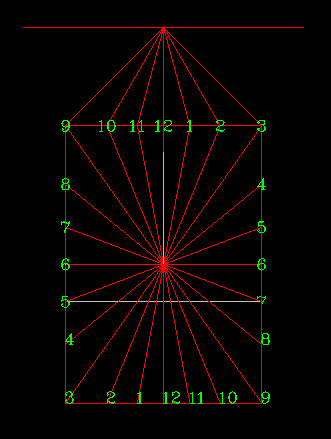
The result looks like this and will be the source data I read into FME:
This is laid out for a sundial at a latitude of 45 degrees north. The gnomon – the sticky-up bit of the sundial that casts the shadow – therefore rises up at 45 degrees too. Reading this into FME I used the SurfaceFootprintReplacer with a random sun angle and got this (click to enlarge):
So that was the sundial created and laid out. The next part was much harder: simulating the actual sun’s position.
Solar Position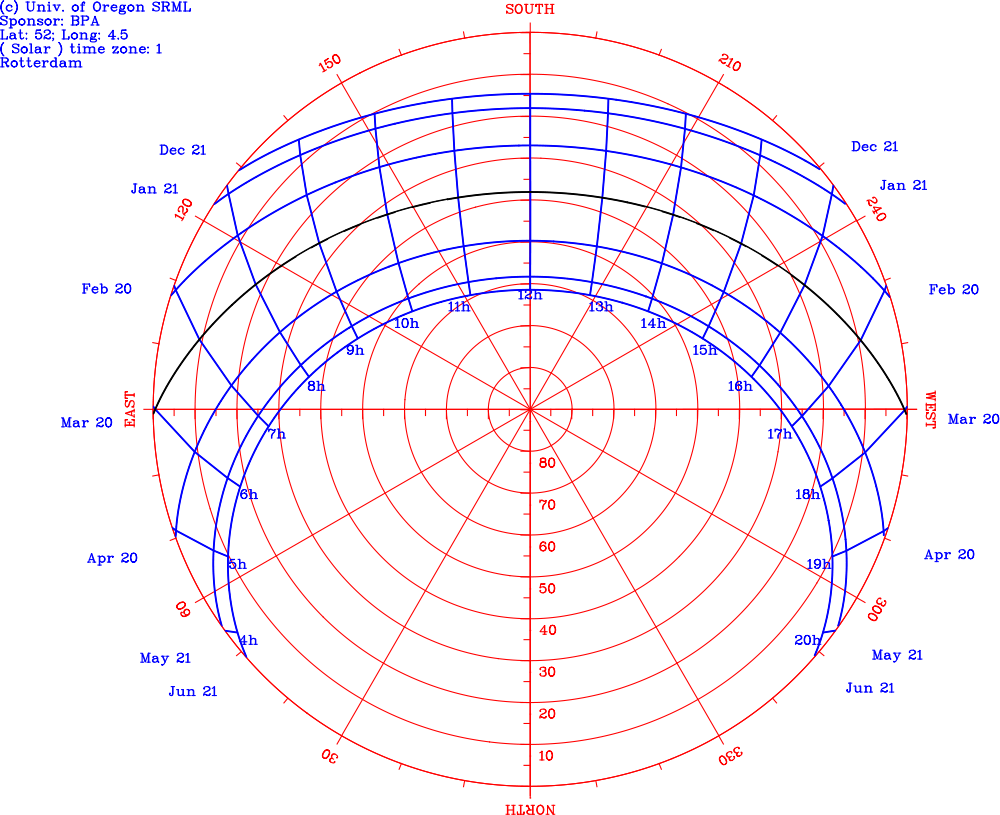
The sun rises in the east, moves through the sky (well, it’s not moving, we are, but you get the point), and sets in the west. At noon – actually ‘Local Apparent Noon’ – the sun is at its highest point, due south.
Technically, if I just want to tell the time, I could simulate the sun’s position as a series of 1,440 point features (one per minute). But I wanted to do the job properly, and actually calculate the real position.
The sun’s position between rising, noon, and setting, depends upon a complex equation involving the latitude and the date. Luckily there are people far smarter than I, and I managed to grab some Python code from this StackOverflow page that will calculate this information.
The code returns azimuth and elevation for the sun at whatever time the code is run. I modified it slightly to account for daylight saving, to read in the latitude and longitude (from FME attributes and published parameters), and to write the results out as FME attributes.
Then, because the SurfaceFootprintReplacer requires an x/y/z vertex for the light position, I converted the azimuth/elevation using some basic trigonometry. Actually, it wasn’t basic enough, because the biggest problem I encountered in the whole project was due to using Sin() instead of Tan() for the elevation – one of those mistakes 3 seconds in the making and 3 hours in the debugging!
Hacking FME
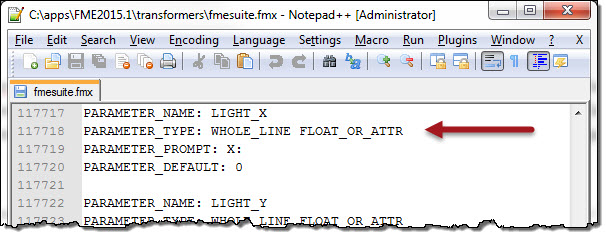
Currently the SurfaceFootprintReplacer only accepts hard-coded values for x/y/z and not attributes. So I had to open up the transformers file and change all three parameter types from FLOAT to FLOAT_OR_ATTR. Before you start looking to try that for other cases, be aware that it’s not a guaranteed solution (I was lucky, it was in this case), it can lead to encoding the underlying factory might not be set up to handle, and this transformer has been updated in FME2016 now anyway. Still, if you want to try my workspaces, you’d have to do the same for now.
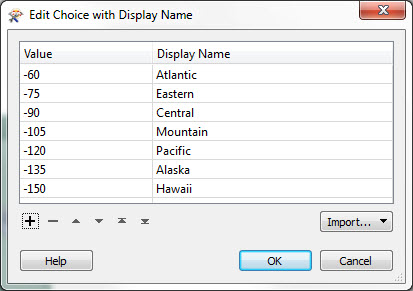
The other thing you would (maybe) need to change is the published parameter for timezone. If you look you’ll notice I only included ones for North America. But you can edit that parameter and add your own time zones, as long as you know the central meridian for that zone.
Remember, meridians west of zero degrees are negative values (e.g. Pacific Time is -120 degrees).
Oddities
One interesting consideration is what happens when the sun goes down. Normally a sundial would be useless at that point, but for a virtual sundial there’s no reason why it can’t tell time 24 hours a day. Of course, when the sun does go down the elevation angle is going to be negative, and I wasn’t sure how the SurfaceFootprintReplacer would handle that.
A sundial usually has 6am on the left, 6pm on the right, with 12 noon at the top. If you think about it, once the sun goes below the horizon, the shadow ought to start going backwards along the sundial, rewinding back to sunrise. But what actually happens is a sudden flip back to the start; so 6pm-6am occurs in the same way as 6am-6pm. I don’t know if that’s the transformer doing that, or my computations, but it’s fine for my purposes. Yes, the shadow would be the same for 11am and 11pm (for example) but if you can’t already tell if it’s day or night, then I really don’t think this is going to help you!
In a similar way, the result might be different for users in the southern hemisphere, but I just haven’t investigated that yet. I don’t think it should – you shouldn’t even need to change the latitude to a negative – but users in Australia, let me know if it’s not telling the correct time for your zones.
3D and Appearances
To improve the look of the output I created a 3d pedestal for the sundial, simply by using Creator transformers to create two box shapes. I applied a stone-like texture (obtained from this web site) and then applied basic colored textures to the gnomon and shadow (making the gnomon brass-like, and the shadow semi-transparent).
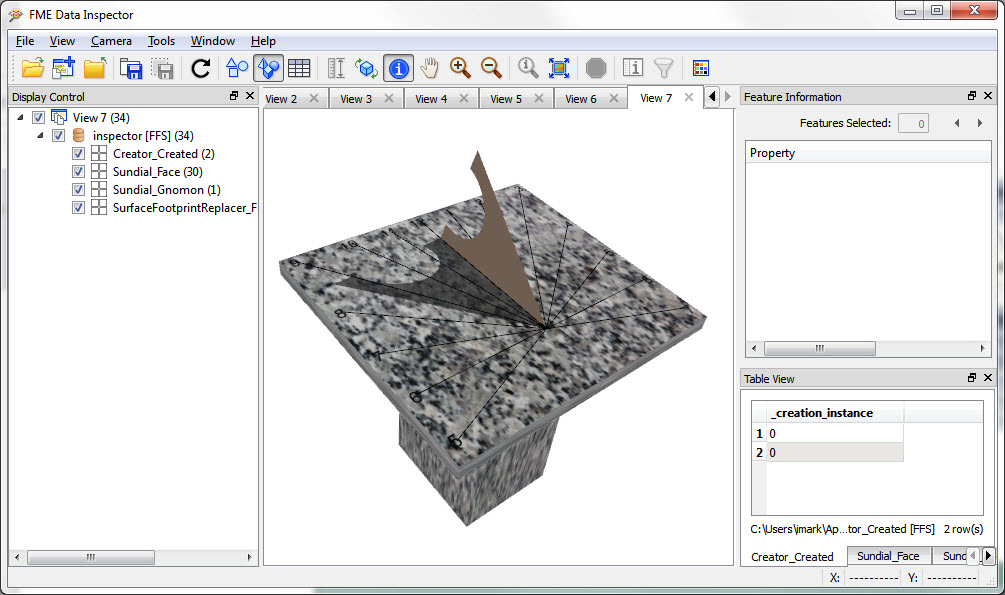
The result? This:
I’m rather pleased with that. Not only does it tell the correct time for my timezone (or any timezone the user selects), I think it looks pretty good too.
Incidentally, you read the sundial using the shadow of the leading edge of the gnomon, so here it is around 8:40 (am or pm).
Conclusion
This was a project that I drifted into. I hadn’t planned to implement it, but then I found the Python code and was hooked.
You can download my workspace (and sundial layout) as a template (for 2015.1) if you would like. Remember that I did have to do a little hack to the transformer definition, without which I don’t think this will run.
Has it got any practical application? Well, I think it’s a great illustration of this new transformer (albeit one that I don’t expect the developers to have considered).
I think too the solar position code could be useful. Perhaps it could be used to calculate solar exposure and the potential for operating solar panels? I know several Safe staff are into solar energy, and I guess some users must be too. So you might find that bit alone of use (in fact I’ll upload that part as a custom transformer to the FME Store when I get a moment)
I’m currently trying to use three.js to visualize the result in a web browser. If it works I’ll post an article and show you how it’s done.
Regards
Image by Clem Rutter, Rochester, Kent. [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons